crypto
DLP-based cryptosystem
0. Lí thuyết nhóm
Cho $G \neq \emptyset$, định nghĩa phép toán $\cdot: G \times G \rightarrow G$
$(G, \cdot)$ là một nhóm (Group) nếu:
- Tiên đề đóng: $\forall a, b \in G: a\cdot b \in G$
- $G$ có phần tử đơn vị: $\exists e \in G: e\cdot a = a\cdot e = a, \forall a \in G$
- $G$ có phần tử nghịch đảo: $\exists a, e \in G: \exists a^{-1} \in G: a \cdot a^{-1} = a^{-1} \cdot a = e$
- $G$ có tính kết hợp: $\forall a, b, c \in G: (a \cdot b) \cdot c = a \cdot (b \cdot c)$
$G$ là nhóm giao hoán (Nhóm Abel) nếu thỏa thêm điều kiện
- $\forall a, b \in G: a\cdot b = b\cdot a$
1. DLP - discrete logarithm problem
Cho $g \in G \equiv \mathbb{Z}^{*}_p, x \in \mathbb{Z}, y \equiv g^x \pmod{p}$. Khi đó bài toán tìm $x$ là một bài toán DLP.
2. Phần tử sinh của nhóm
Ví dụ: Xét nhóm $\left(\mathbb{Z}^{*}_7, \cdot_7\right)$ (tạm hiểu $\cdot_7$ là phép mũ $7^x\ \forall x \in \mathbb{Z}^{*}_7$)
Với $2 \in \mathbb{Z}^{*}_7$, tập các giá trị có thể có là ${1, 2, 4}$:
- $2^0 \equiv 1 \pmod 7$
- $2^1 \equiv 2 \pmod 7$
- $2^2 \equiv 4 \pmod 7$
- $2^3 \equiv 1 \pmod 7$ (quay lại ban đầu) ..
Với 3 thì khác, tập giá trị có thể có là ${1, .., 6}$.
Gọi $\text{ord}\left(g\right)$ là bậc của $g \in G$. Đặt $\left|G\right| = n$, nếu $\text{ord}\left(g\right) = n - 1$ thì $g$ là một phần tử sinh của $G$.
Thuật toán phía dưới tìm nhanh các phần tử sinh của $n$.
def naive_generator_list(n):
result = []
for i in range(2, n):
is_generator = True
power = 1
generated = []
while 1:
m = (i ** power) % n
if (m not in generated):
generated.append(m)
else: break
power += 1
if len(generated) != n - 1: is_generator = False
if is_generator: result.append(i)
return result
print('Generators of Z_11: ', naive_generator_list(11))
print('Generators of Z_13: ', naive_generator_list(13))
print('Generators of Z_17: ', naive_generator_list(17))
Generators of Z_11: [2, 6, 7, 8]
Generators of Z_13: [2, 6, 7, 11]
Generators of Z_17: [3, 5, 6, 7, 10, 11, 12, 14]
Một thuật toán tìm nhanh phần tử sinh
Cho $p$ là một số nguyên tố có dạng $p = 2q + 1$ (như ta đã tạo trong RSA) $\Rightarrow (p - 1)$ không phải là một số nguyên tố.
Ta có thể biểu diễn $(p - 1) = s_1^{e_1}s_2^{e_2}..s_m^{e_m} (e_i \geq 1)$. Thuật toán tìm nhanh phần tử sinh được miêu tả như sau:
- Lấy random một số nguyên $x \in (2, p)$
-
$\forall s_i \in [1, m]$:
Nếu $x^{\frac{(p - 1)}{s_i}} \equiv 1 \pmod p$ thì $x$ không phải là phần tử sinh của $p$, trở lại bước 1.
- $x$ là một phần tử sinh, return x.
Thuật toán trình bày bên dưới.
import random
from functools import reduce
# For consistent output
random.seed(42)
def factors(n):
return set(reduce(list.__add__,
([i, n//i] for i in range(1, int(n**0.5) + 1) if n % i == 0)))
def find_random_generator(n):
while 1:
x = random.randrange(2, n)
is_generator = True
for i in factors(n - 1):
if i == 1: continue
k = (n - 1) // i
if (x ** k) % n == 1:
is_generator = False
break
if is_generator: return x
print(find_random_generator(11))
print(find_random_generator(13))
print(find_random_generator(17))
2
6
5
Key Exchange Protocol (Diffie - Hellman)
Điểm chính: thống nhất 1 bí mật chung giữa người gửi và người nhận.
Pha 0: Chuẩn bị
- Tạo ngẫu nhiên $p$ là một số nguyên tố có độ an toàn $\lambda$.
- Chọn $g$ là một phần tử sinh của $p$.
Pha 1: Mã hóa & giải mã
- Phía người gửi:
- Chọn ngẫu nhiên $x \in (2, p)$.
- Tạo khóa $k_A \equiv g^x \pmod p$
- Gửi khóa $k_A$ cho người nhận.
- Phía người nhận:
- Chọn ngẫu nhiên $y \in (2, p)$.
- Tạo khóa $k_B \equiv g^y \pmod p$
- Gửi khóa $k_B$ cho người gửi.
Khi đó khóa $k$ để mã hóa & giải mã được tính như sau: $k \equiv k_B^x \equiv k_A^y \pmod p$
Ví dụ 1: Mã hóa đối xứng
Phía người gửi tính $c \equiv mk \pmod p$
Phía người nhận tính $m \equiv ck^{-1} \pmod p$
Ví dụ 2: Mã hóa bất đối xứng (Elgamal)
Giả sử Alice gửi mã và Bob giải mã, vậy Bob sẽ là người tạo khóa.
- Phía người nhận:
- Chọn $p, g$ như Pha 0 bên trên.
- Chọn ngẫu nhiên $d \in (2, p)$.
- Tính khóa mã $e \equiv g^d \pmod p$
- Gửi bộ $p, g, e$ cho người gửi.
- Phía người gửi:
- Nhận $p, g, e$.
- Chọn ngẫu nhiên $x \in (2, p)$.
- Tính $c_1, c_2$:
- $c_1 \equiv g^x \pmod p$
- $c_2 \equiv me^x = mg^{dx} \pmod p$
- Gửi $c = (c_1, c_2)$ cho người nhận.
Người nhận giải mã bằng cách tính $m \equiv (c_1^d)^{-1}c_2 \pmod p$
Chú ý: Chọn $p$ quá nhỏ sẽ dẫn đến trường hợp encrypt ra các kí tự bị collision.
Giải bài toán logarithm rời rạc
Các thuật DLP dựa vào độ khó của bài toán logarithm rời rạc (i.e cho $g, h, p$, tìm $x$ sao cho $g^x \equiv h \pmod p$). Giải bài toán logarithm rời rạc, thường dùng là thuật toán Index Calculus.
Thuật toán Index Calculus
1. B-Smooth
$n \in \mathbb{Z}$ là một số $B$-smooth khi và chỉ khi $\displaystyle n = \prod_{p_i \in \mathbb{P}} p_i (p_i \leq B)$ (với $\mathbb{P}$ là tập các số nguyên tố).
2. Thuật toán
Cho $g^x \equiv h \pmod p, g, p$. Tìm $x$?
- Giải $g^x \equiv l \pmod p\ (l \leq B)$
- Tìm $k$ sao cho $hg^{-k}$ là một số $B$-smooth
$\displaystyle \iff hg^{-k} = \prod_{p_i \in \mathbb{P}} p_i^{e_{p_i}} \pmod p\ (p_i \leq B) \ \iff \log_{g}h = k + \sum_{p_i \leq B} e_{p_i} \log_{g} p_i \pmod p $
3. Ví dụ
Giải phương trình đồng dư $6^x = 57 \pmod{107}$
- Chọn $B = 7 \Rightarrow \mathbb{B} = {2, 3, 5, 7}$
- Thử-và-sai nhiều lần:
- Chọn $k = 24 \Rightarrow 6^k \equiv 42 \pmod{107} = 2\times3\times7$
- Chọn $k = 6 \Rightarrow 6^k \equiv 4 \pmod{107} = 2^2$
- Chọn $k = 33 \Rightarrow 6^k \equiv 15 \pmod{107} = 3\times5$
- Chọn $k = 34 \Rightarrow 6^k \equiv 90 \pmod{107} = 2\times3^2\times5$
Điều này tương đương với
\[\begin{cases} 24 \equiv \log_{6}2 + \log_{6}3 + \log_{6}7 \pmod{107}\\ 6 \equiv 2\log_{6}2 \pmod{107}\\ 33 \equiv \log_{6}3 + \log_{6}5 \pmod{107}\\ 34 \equiv \log_{6}2 + 2\log_{6}3 + \log_{6}5 \pmod{107} \end{cases}\]Lần lượt đặt $\log_{6}2 = a, \log_{6}3 = b, \log_{6}5 = c, \log_{6}7 = d$, ta có hệ 4 phương trình 4 ẩn. Giải hệ phương trình, ta thu được các nghiệm
\[\begin{cases} a = \log_{6}2 = 3\\ b = \log_{6}3 = 104\\ c = \log_{6}5 = 35\\ d = \log_{6}7 = 23 \end{cases}\](Chú ý đây không phải phép logarit thông thường!)
- Tiếp tục thử-sai nhiều lần: chọn $u$ sao cho $hg^u$ là một số $B$-smooth
Chọn $u = 38 \Rightarrow hg^u \equiv 35 = 5\times7 \pmod{107}$
Lấy logarithm 2 vế cho $6$:
$\log_{6}(57\times 6^{38}) = \log_{6}5\times \log_{6}7 \iff \log_{6}57 + 38 = \log_{6}5 + \log_{6}7$. Mà $6^x \equiv 57 \pmod{107} \Rightarrow x \equiv \log_{6}57 = \log_{6}5 + \log_{6}7 - 38 = 35 + 23 - 38 = 20$.
Đường cong Elliptic
Định nghĩa:
Nhóm $(\mathbb{G}, +)$ là nhóm các điểm nằm trên đường cong Elliptic $(E): y^2 = x^3 + ax + b$ với:
- $\mathbb{G} = {P(x, y) \in (E), \forall x, y \in \mathbb{Z}_p}$
- $+:\mathbb{G} \times \mathbb{G}\to \mathbb G,\; P + Q\mapsto R $ (Chọn 2 điểm $P, Q \in (E)$, đường thẳng đi qua $P, Q$ cắt $E$ tại điểm thứ 3 là $Z$. Lấy $R$ là đối xứng của $Z$ qua $Ox$).
- Nếu $P$ và $Q$ không cắt $(E)$ ở điểm thứ 3 thì $P + Q = O$ với $O$ là điểm vô cực.
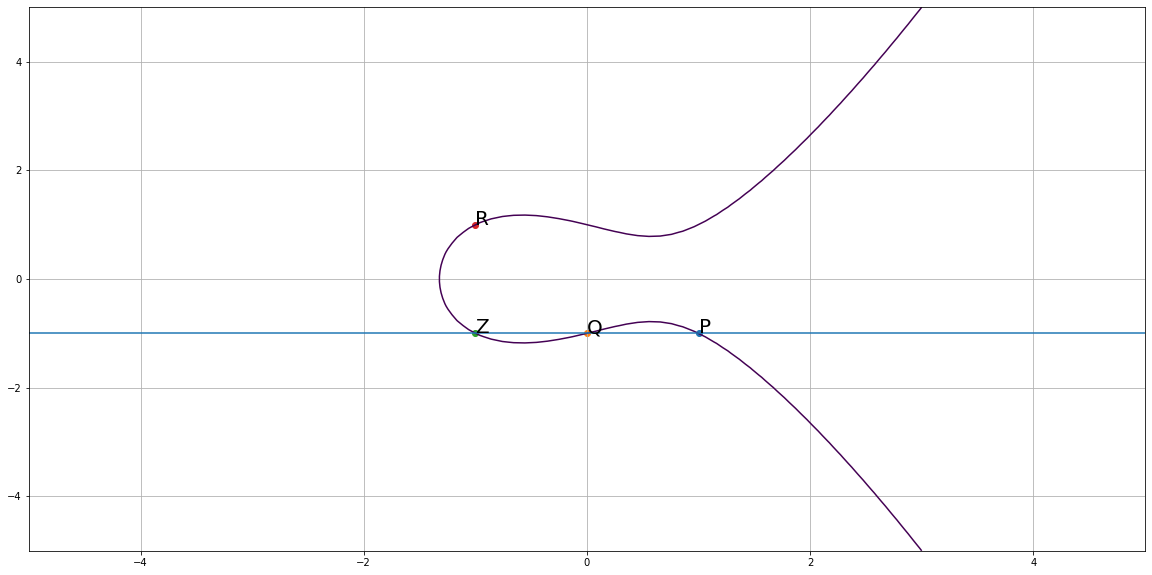
Hình bên dưới là biểu diễn của đường cong Elliptic $(E): y^2 = x^3 - x + 1, P = (1, -1), Q = (0, -1), R = P + Q$.
import numpy as np
import matplotlib.pyplot as plt
a = -1
b = 1
y, x = np.ogrid[-5:5:100j, -5:5:100j]
plt.figure(figsize=(20, 10))
plt.contour(x.ravel(), y.ravel(), pow(y, 2) - pow(x, 3) - x * a - b, [0])
plt.grid()
plt.scatter(1, -1)
plt.annotate('P', (1, -1), size = 20)
plt.scatter(0, -1)
plt.annotate('Q', (0, -1), size = 20)
plt.axhline(y = -1)
plt.scatter(-1, -1)
plt.annotate('Z', (-1, -1), size = 20)
plt.scatter(-1, 1)
plt.annotate('R', (-1, 1), size = 20)
plt.show()
Hệ mã ECC (Elliptic Curve Cryptosystem)
- Chọn $p \in \mathbb{P}$ và $(E)$ là một đường cong Elliptic; Chọn $G \in (E)$.
- Chọn $d$ ngẫu nhiên, $e = dG = G + G + .. + G$ ($d$ lần).
- Pha mã hóa: chọn $y$ ngẫu nhiên, $c_1 = yG, c_2 = M + ye$ ($M$ là tin cần mã hóa).
- Pha giải mã: $M = c_2 - dc_1$.